
快速排序
快速排序效率高,空间复杂度底,在工作中一般是用的最多的排序算法,所以需要掌握。
在看快速排序之前,先看一下另一个比快排简单点的问题,就是荷兰国旗问题
给定一个数组arr,和一个数num,请把小于num的数放在数组的左边,等于num的数放在数组的中间,大于num的数放在数组的右边。
要求额外空间复杂度O(1),时间复杂度O(N)
解决思路:
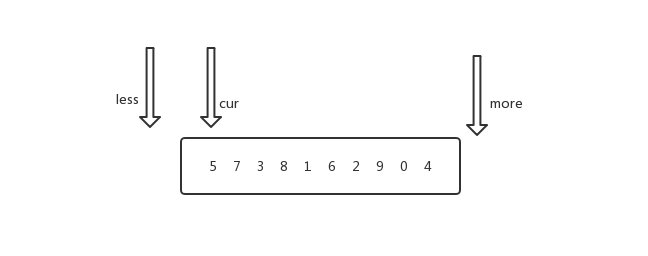
准备准备三个指针less、more、cur
- less指针,从数组的第一个元素的前一个位置开始,第一个元素的位置为0,所以less从-1开始
- more指针,从数组最后一个元素的后一个位置开始,最后一个元素的位置是数组长度减一位置,所以more的值就是数组的长度
- cur指针,当前比较的元素的位置,从第一个元素开始比较,也就是从0开始
- 如果当前元素小于num,less的后一个位置的元素跟cur位置的元素交换。交换完成之后,当前位置cur加一,比较下一个元素
- 如果当前元素大于num,more的前一个元素跟cur位置的元素交换。交换完成之后,此时交换回来的元素我们不知道它大于num还是小于num,所以cur位置不变,继续比较
- 如果当前元素的值等于num,cur直接加一,比较下一个。
代码如下
1 | public static int[] partition(int[] arr, int num) { |
快速排序跟荷兰国旗算法的思想差不多,不同的是荷兰国旗算法是给了一个num值用来比较,快速排序中,我们自己从数组中随便找一个数来作为比较值。数组分成两部分之后,这两部分按照同样的方式递归在分自己,最后完成排序
解决思路
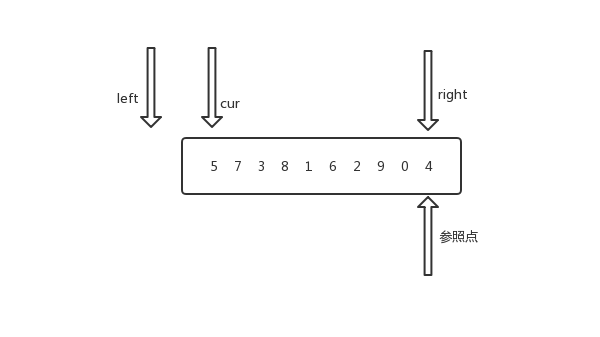
- 首先选一个参照点,一般选择数组的最后一个值当做参照点
- 之后的交换思路就跟荷兰国旗思路一样了
- 需要注意,如果需要排序的数据本来就是一个有序的数组,那么如果一直选择最后的点作为参考点,那么每次分区得到的两个区间是不相等的,每次都要进行n次分区操作,每次分区大约扫描n/2个元素,时间复杂度会退化为O(N²)
- 解决方式,每次不在取最后一个,从数组中随机取一个数,然后跟最后一个元素交换,在按照前的方式循环。改成随机事件,就从概率上降低了时间复杂度
代码如下
代码中直接使用left这个变量代替cur,可以省一个变量
1 | public static void quickSort(int[] arr) { |